Euclidean algorithms (Basic )

GCD of two numbers is the largest number that divides both of them. A simple way to find GCD is to factorize both numbers and multiply common factors.

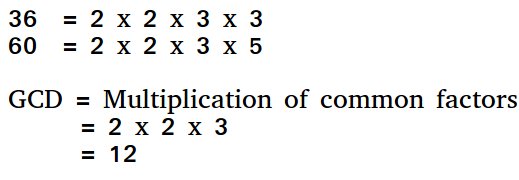
Basic Euclidean Algorithm for GCD
The algorithm is based on below facts.

• If we subtract smaller number from larger (we reduce larger number), GCD doesn’t change. So if we keep subtracting repeatedly the larger of two, we end up with GCD.
• Now instead of subtraction, if we divide smaller number, the algorithm stops when we find remainder 0.

Below is a recursive function to evaluate gcd using Euclid’s algorithm.

• CPP
• C
• Java
• Python3
• C#
• PHP

// C++ program to demonstrate // Basic Euclidean Algorithm #include <bits/stdc++.h> using namespace std;    // Function to return  // gcd of a and b int gcd(int a, int b) {     if (a == 0)         return b;     return gcd(b % a, a); }    // Driver Code int main() {     int a = 10, b = 15;     cout << "GCD(" << a << ", "           << b << ") = " << gcd(a, b)                          << endl;     a = 35, b = 10;     cout << "GCD(" << a << ", "           << b << ") = " << gcd(a, b)                          << endl;     a = 31, b = 2;     cout << "GCD(" << a << ", "           << b << ") = " << gcd(a, b)                          << endl;     return 0; }    // This code is contributed  // by Nimit Garg

Output :

GCD(10, 15) = 5
GCD(35, 10) = 5
GCD(31, 2) = 1

Time Complexity: O(Log min(a, b)