“বিগ মোড অ্যালগোরিদম(Big Mod Algorithm)”
অনেক সময় বিভিন্ন প্রবলেম সল্ভ করার সময় আমাদের প্রায়ই বিগ মোড করার প্রয়োজন হয়। যেমন, বলা হল (2^30)%11 এর ভ্যালু কি। এর জন্য আমাদের বিগ মোড অ্যালগোরিদম জানা প্রয়োজন।
বিগ মোড অ্যালগোরিদমকে modulus multiplication এর ব্যাসিক প্রপার্টির extension বলা যায়। বিগ মোড অ্যালগোরিদমের ভেতরে যাওয়ার আগে আমাদের modulus arithmetic এর একটা সহজ প্রপার্টি জানা প্রয়োজন।
Modulus arithmetic অনুসারে (a*b)%c কে এইভাবে লেখা যায়ঃ
(a*b)%c = ((a%c)*(b%c))%c
যেমন, (15*16)%7 = 2
আবার, (15%7 * 16%7) % 7 = (1 * 2) % 7 = 2%7 = 2
বিগ মোড অ্যালগোরিদমের জন্য শুধুমাত্র এই সুত্রটাই যথেষ্ট।
2^30 কে আমরা ২ভাগে ভাগ করতে পারিঃ (2^15)*(2^15)
তাহলে, (a*b)%c = ((a%c)*(b%c))%c এই সূত্র অনুসারে,
(2^30)%11 = ( (2^15) * (2^15) )%11
= ( ( (2^15) % 11 ) * ( (2^15) % 11 ) )%11
আমরা 2^15 কে আবার একইভাবে ২ভাগে ভাগ করতে পারিঃ 2*(2^14)
এখন, (2^15)%11 = ( (2%11) * ( (2^14)%11 ) ) % 11
এভাবে কাজ করতে থাকে আমরা যেটা পাই,
শুরতে, 2^30 = (2^15) * (2^15)
Then, 2^15 = 2 * (2^14)
Then, 2^14 = (2^7) * (2^7)
Then, 2^7 = 2 * (2^6)
Then 2^6 = (2^3) * (2^3)
Then 2^3 = 2 * (2^2)
Then 2^2 = 2*2
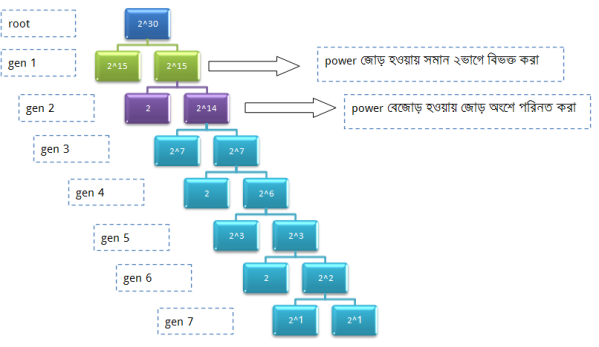
বিষয়টা অনেকটা এরকমঃ
এখন আমরা দেখব কিভাবে এই figure থেকে (2^30)%11 এর ভ্যালু পাওয়া যায়।
আমরা gen 7 থেকে আমাদের কাজ শুরু করব।
gen 7: ((2^1)*(2^1))%11
2^1 = 2
2%11 = 2
সুতরাং gen 7 = ((2^1)*(2^1))%11
= (2*2)%11
= 4
gen 6: (2 * (2^2)) %11 = ( (2%11) * ((2^2)%11) )%11
এখানে, 2%11 = 2
(2^2)%11 = ((2^1)*(2^1))%11 [যেটা প্রকতপক্ষে gen 7]
= 4 [gen 7 থেকে প্রাপ্ত]
সুতরাং gen 6 = (2 * (2^2)) %11 [লক্ষণীয়, 2 * (2^2) = 2^3]
= ( (2%11) * ((2^2)%11) )%11
= ( 2 * 4 ) % 11
= 8
gen 5: ((2^3)*(2^3))%11 = ( (2^3)%11) * ((2^3)%11) )%11
এখানে, ( (2^3)%11) = (2 * (2^2)) %11 [যেটা প্রকতপক্ষে gen 7]
= 8
তাহলে, gen 5 = ((2^3)*(2^3))%11
= ( (2^3)%11) * ((2^3)%11) )%11
= ( 8 * 8 ) % 11
= 9
gen 4: (2 * (2^6)) %11 = ( (2%11) * ((2^6)%11) )%11
এখন, (2^6)%11 = ((2^3)*(2^3))%11
= gen 5
= 9
তাহলে, gen 4 = (2 * (2^6)) %11
= ( (2%11) * ((2^6)%11) )%11
= ( 2 * 9 ) % 11
= 7
gen 3: ((2^7)*(2^7))%11 = ( (2^7)%11) * ((2^7)%11) )%11
এখানে, ( (2^7)%11) = (2 * (2^6)) %11 [যেটা প্রকতপক্ষে gen 4]
= 7
তাহলে, gen 3 = ((2^7)*(2^7))%11
= ( (2^7)%11) * ((2^7)%11) )%11
= ( 7 * 7 ) % 11
= 5
gen 2: (2 * (2^14)) %11 = ( (2%11) * ((2^14)%11) )%11
এখন, (2^14)%11 = ((2^7)*(2^7))%11
= gen 3
= 5
তাহলে, gen 2 = (2 * (2^14)) %11
= ( (2%11) * ((2^14)%11) )%11
= ( 2 * 5 ) % 11
= 10
gen 1: ((2^15)*(2^15))%11 = ( (2^15)%11) * ((2^15)%11) )%11
এখানে, ( (2^15)%11) = (2 * (2^14)) %11 [যেটা প্রকতপক্ষে gen 2]
= 10
তাহলে, gen 1 = ((2^15)*(2^15))%11
= ( (2^15)%11) * ((2^15)%11) )%11
= ( 10 * 10 ) % 11
= 1
root: (2^30)%11 = ((2^15)*(2^15))%11
= gen 1
= 1
সুতরাং আমরা বলতে পারি, (2^30)%11 = 1
বিষয়টাকে খুব সহজে coding এ রুপান্তরিত করা যায়; এর জন্য আমরা recursion এর সাহায্য নেব ।
coding এ রুপান্তরের জন্য আমাদের ২টা বিষয় check করতে হবে : power জোড় না বেজোড় ।
Big Mod এর Function টা এরকম ঃ
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int big_mod(int base, int power, int mod){ if(power==0) return 1; //কোন কিছুর power 0 হলে তার মান 1 হয়ে যায় else if(power%2==1) //power বেজোড় হলে { int p1 = base % mod; int p2 = (big_mod(base,power-1,mod))%mod; return (p1*p2)%mod; } else if(power%2==0) //power জোড় হলে { int p1 = (big_mod(base,power/2,mod))%mod; return (p1*p1)%mod; }} |
Big Mod সংক্রান্ত প্রব্লেমঃ



No comments